중등 1학년 수학 > 일차방정식의 활용 > 소금물 농도, 소금의 양 기초 연습문제 프린트 학습지
일차방정식의 활용 문제 유형 중에서 '소금물' 문제는 많은 학생들이 어려워 하는 유형인데요, 소금물의 농도를 구하는 공식과 소금의 양을 구하는 공식을 암기해야 문제를 풀 수 있어요.
기본적으로 공식은 뼈대가 되는 개념을 잘 알아야 오래 기억할 수 있습니다.
소금물의 농도는 %단위를 사용하는데요, %단위를 '백분율'이라고 불러요.
백분율이 무엇일까요?
백분율은 비율에 100을 곱한 값입니다. 그럼 비율이 무엇인지도 알아야하죠.
비율은 비교하는 양과 기준이 되는 양을 분수로 나타낸 수예요.
$$비율=\dfrac{비교하는 양}{기준이 되는 양}$$
가령 한 반에 학생이 25명인데, 그 중에 안경을 쓴 사람이 10명이라면.
비교하는 양 : 10, 기준이 되는 양 : 25 이므로 안경을 쓴 학생의 비율은 $\dfrac{10}{25}=\dfrac{2}{5}$이 됩니다.
$$백분율(\%)=비율\times{100}$$
이므로 만약 몇 %의 학생이 안경을 썼는지 묻는다면, 비율에 100을 곱한 $\dfrac{10}{25}\times{100}=40\%$가 안경을 쓰고 있다고 말할 수 있어요.
소금물의 농도도 이와 같은 구조를 가지고 있어요.
$\cdot$ 소금물의 농도 공식
$$소금물의\ 농도(\%)={비율}\times{100}=\dfrac{소금의\ 양}{소금물의\ 양}\times{100}$$
%단위를 사용하기 때문에 비율×100 으로 구성되어 있습니다.
그럼 소금물의 농도에서 말하는 '비율'은 다음과 같이 구성되어 있다는 것을 기억하시기 바래요.
소금의 양 : 소금물의 양 → $\dfrac{소금의\ 양}{소금물의\ 양}$
그럼 소금물의 양이란 무엇일까요?
소금물의 양 = 소금의 양 + 물의 양
만약 100g의 물에 20g의 소금을 넣는다면 소금물의 양은 120g이 됩니다. 이러한 세부적인 구성을 정확히 알고 있어야 문제를 해석하는 힘이 생긴답니다.
$\cdot$ 소금의 양 공식 만들기
소금의 양 공식은 소금물의 농도 공식을 변형한 식이에요.
$$소금물의\ 농도=\dfrac{소금의\ 양}{소금물의\ 양}\times{100}$$
양변에 100을 나누면,
$$\dfrac{소금물의\ 농도}{100}=\dfrac{소금의\ 양}{소금물의\ 양}$$
양변에 소금물의 양을 곱하면,
$$\dfrac{소금의\ 양\times{소금물의\ 농도}}{100}=소금의\ 양$$
그러면 이제 소금물의 농도, 소금물의 양에 대한 개념을 바로 적용할 수 있는 가벼운 문제를 풀어보도록 할게요.

문제를 그림으로 나타내면 다음과 같아요. 소금물 문제는 항상 시각화하면서 풀면 좋습니다.
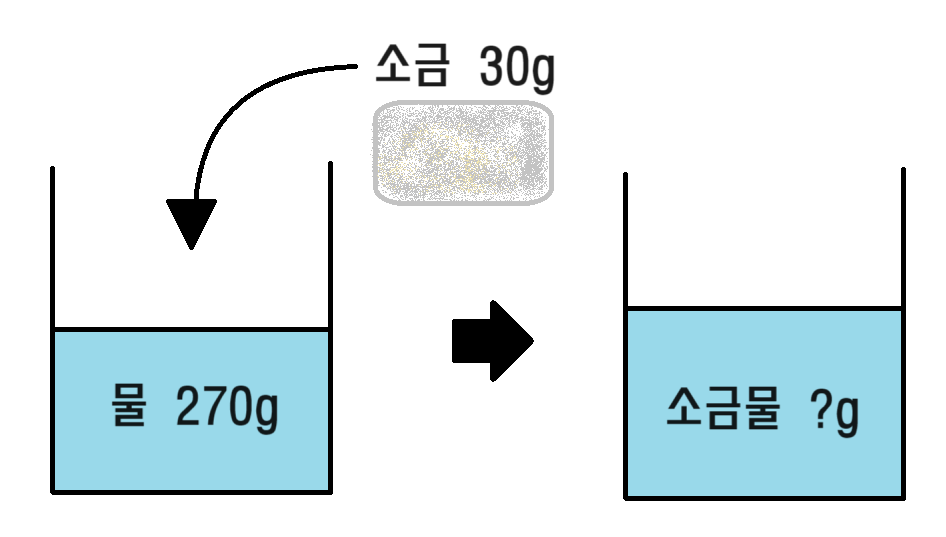
위 그림에서 소금물의 양은 300g이 됩니다.
그럼 이제 소금물의 농도 공식에 적용해볼까요?
소금물의 농도$=\dfrac{30}{300}\times{100}=10(\%)$
정답은 10%가 됩니다.
다음 문제도 풀어보겠습니다.

소금의 양을 묻는 문제예요. 소금의 양 공식을 떠올려봅시다.
$소금의 양=\dfrac{소금물의\ 양\times{소금물의\ 농도}}{100}$
공식에 대입하면
$소금믜 양=\dfrac{28\times{250}}{100}=70(g)$
정답은 70g입니다.
이렇게 소금물의 농도 공식과 소금의 양 공식을 공부하고, 개념을 적용하는 간단한 문제까지 풀어봤습니다.
아래는 개념 문제를 충분히 연습할 수 있는 '모두매쓰' 사이트에서 만든 문제입니다.
모두매쓰에 접속하시면 무한히 문제를 생성하여 프린트할 수 있으니, 많이 이용하시길 추천드립니다.
중등 1학년 수학 > 일차방정식의 활용 > 소금물 농도, 소금의 양 기초 연습문제 프린트 학습지
'중등 수학' 카테고리의 다른 글
| 중등 1학년 수학 > 일차방정식의 활용 > 원가, 정가, 이익 개념과 기초 연습문제 프린트 학습지 (0) | 2024.07.16 |
|---|---|
| 중등 1학년 수학 > 일차방정식의 활용 > 거리, 속력, 시간 공식과 기초 연습문제 프린트 학습지 (0) | 2024.07.16 |
| 중등 2학년 수학 > 삼각형의 내심과 외심 > 내심과 외심이 포함된 삼각형의 각의 크기 구하기 연습문제 프린트 학습지 (0) | 2024.07.15 |
| 중등 2학년 수학 > 이등변삼각형 > 시험 기출문제 필수 유형 연습문제 풀이 프린트 학습지 (0) | 2024.07.15 |
| 중등 2학년 수학 > 삼각형의 내심과 외심 > 삼각형의 외심의 성질 연습문제 프린트 학습지 (0) | 2024.07.14 |





