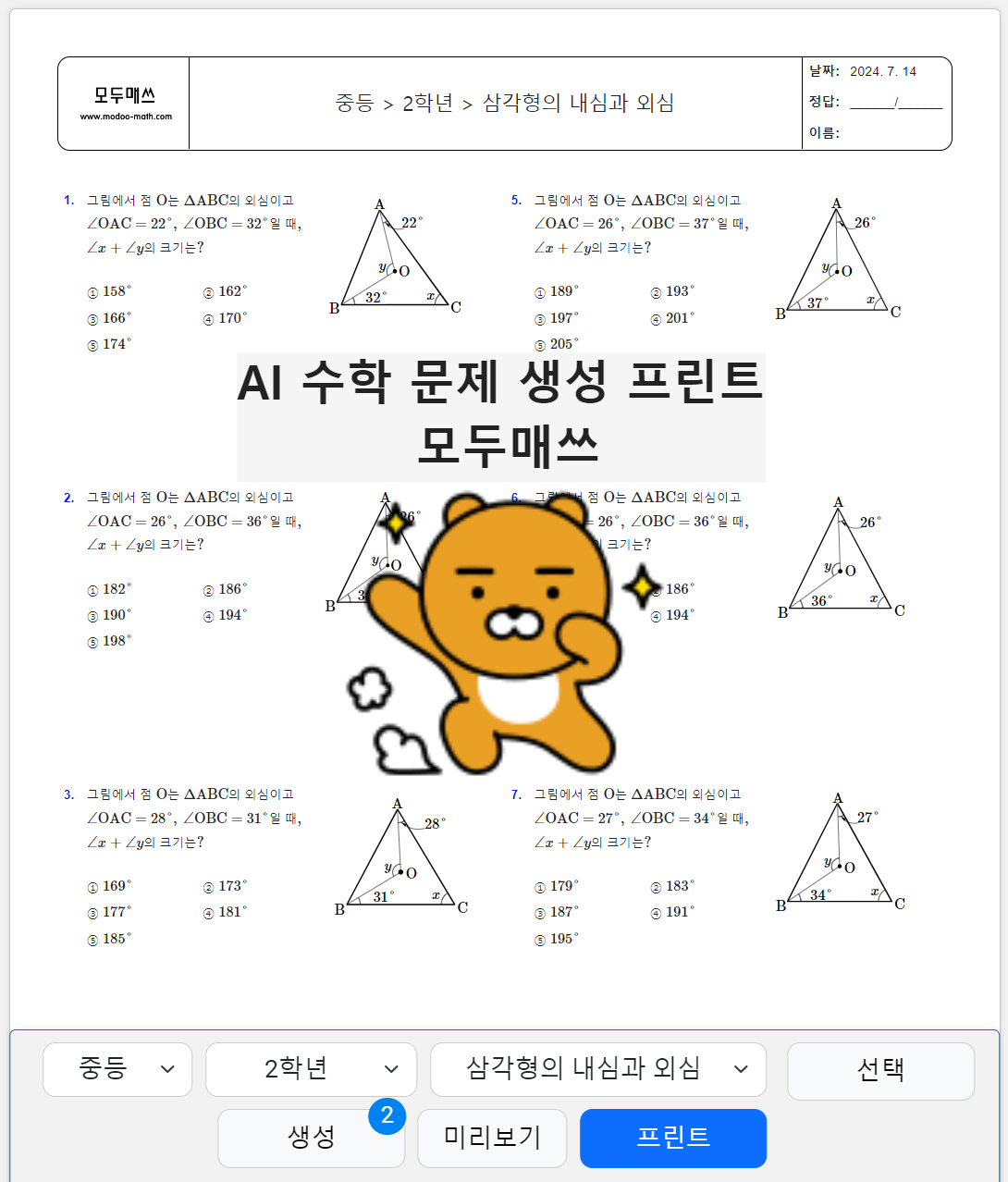
중등 2학년 수학 > 삼각형의 내심과 외심 > 삼각형의 외심의 성질 연습문제 프린트 학습지
외심
삼각형의 각 변의 수직이등분선의 교점
외심의 성질
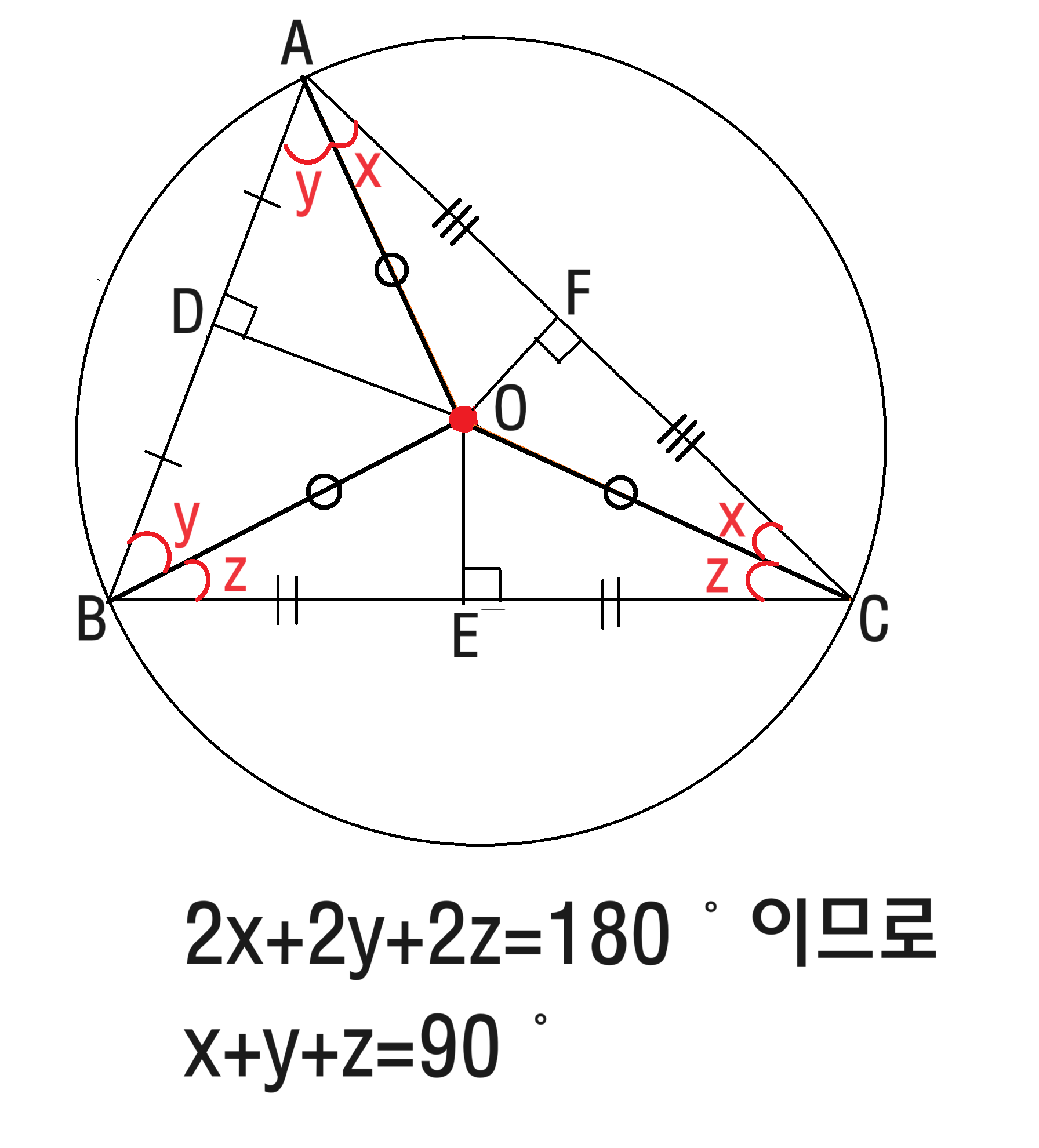
외심에서 각 꼭짓점에 이르는 거리가 모두 같다.
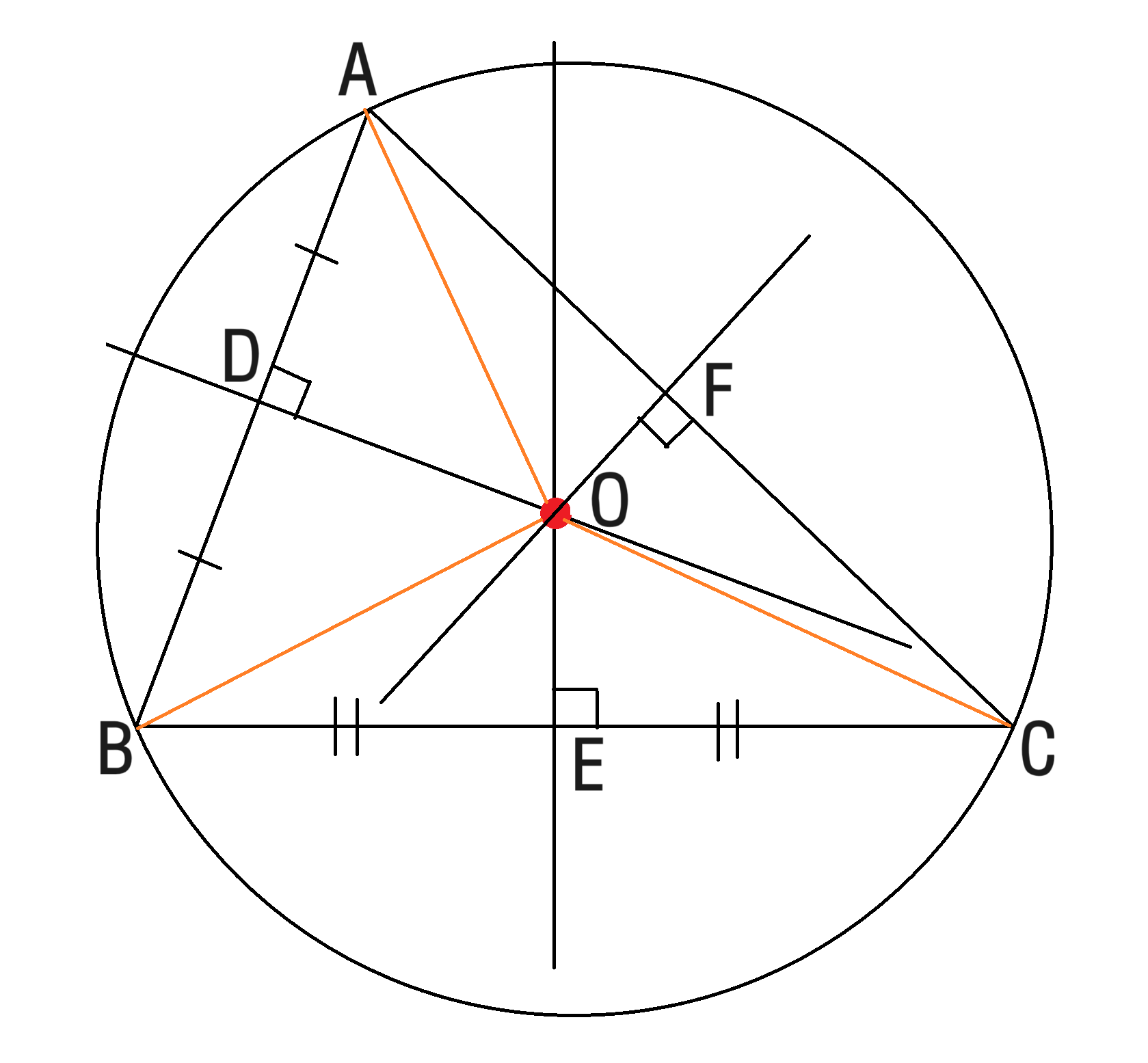
$\overline{AO}=\overline{BO}=\overline{CO}$이므로 아래 세 쌍의 삼각형끼리 RHS합동입니다.
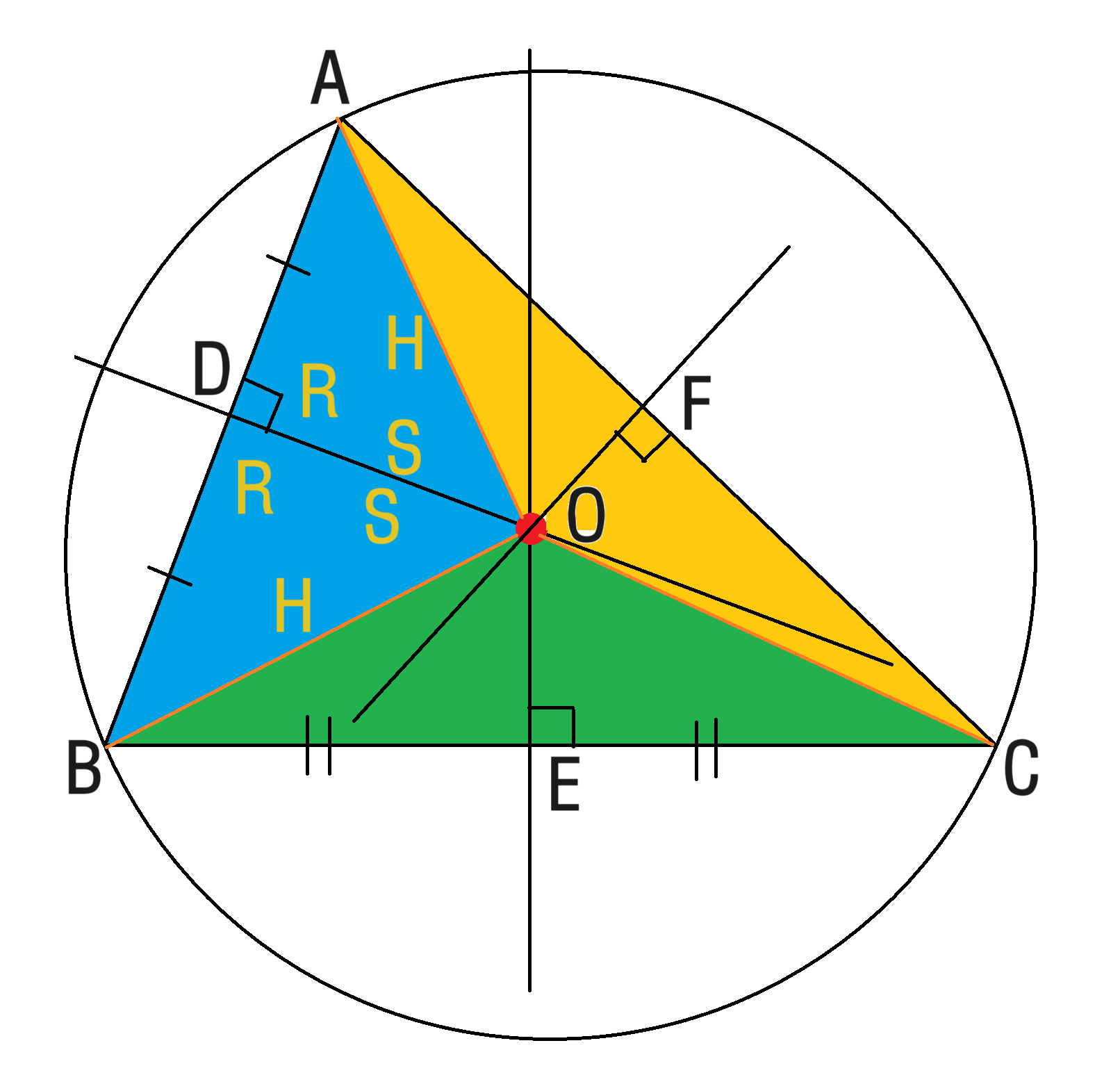
이러한 내용을 바탕으로 아래와 같은 그림을 설명할 수 있어요.
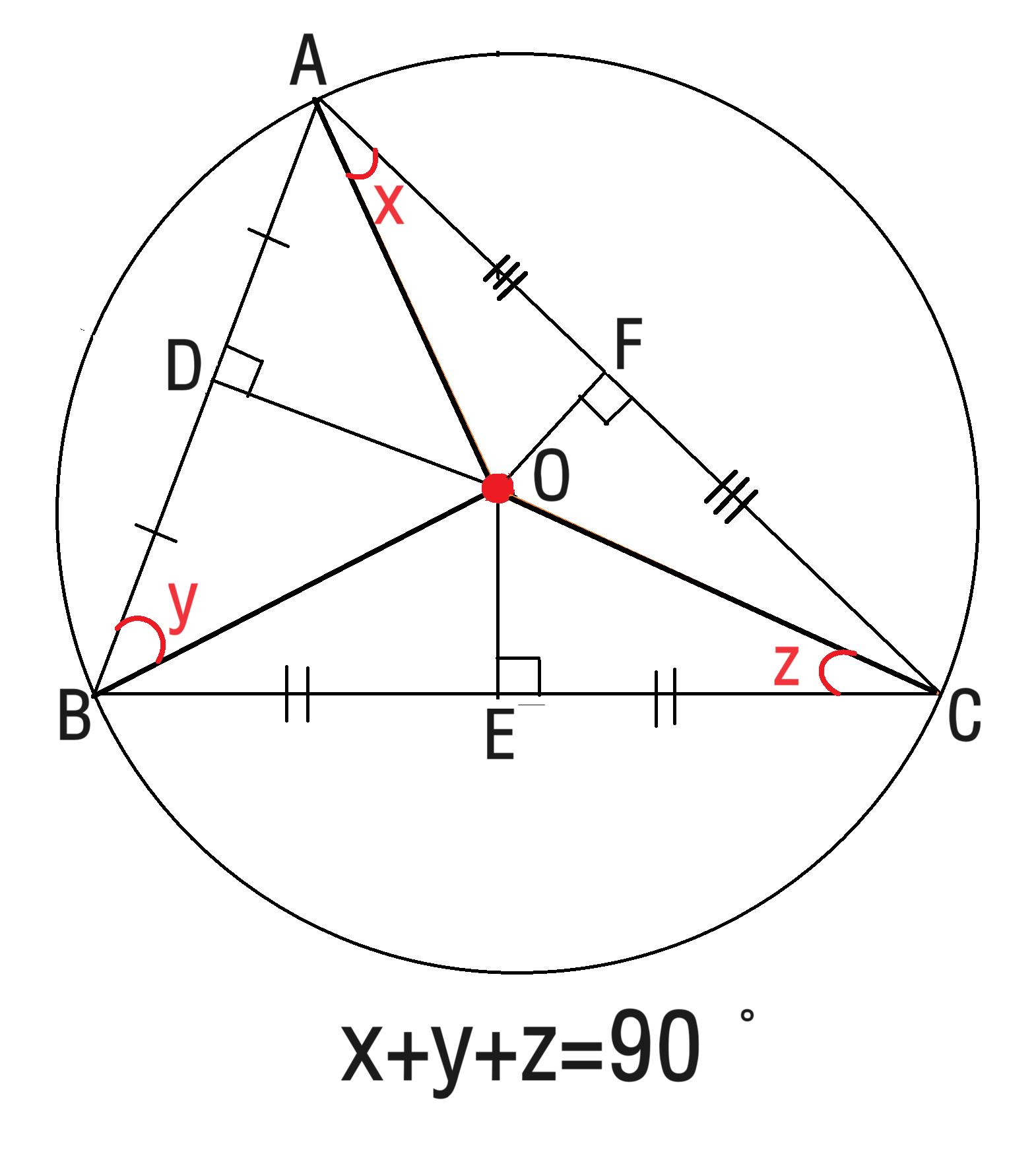
위 식이 성립하는 이유는 아래와 같아요. 세 쌍의 직각삼각형이 합동이므로 세 개의 이등변삼각형이 각각 x, y, z를 하나씩 더 가지고 있고, 모두 더하면 삼각형의 세 내각의 합인 180˚와 같기 때문입니다.
이제 개념을 활용한 문제를 풀어보도록 할게요.
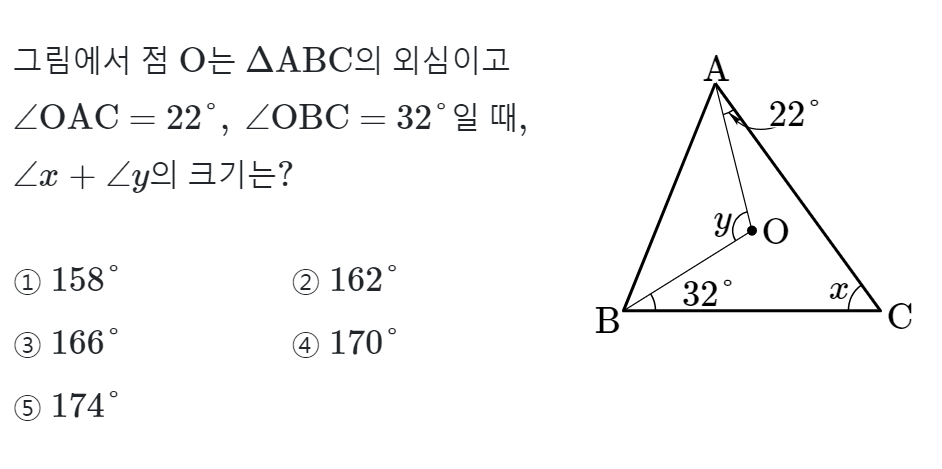
우선 삼각형의 외심 O에서 꼭짓점C에 보조선을 그으면, 아래와 같이 $x$의 각을 구할 수 있습니다.
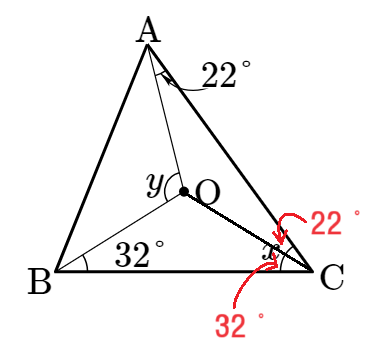
$x=32˚+ 22˚ = 54˚ $입니다. 이제 남은 $y$의 각을 구하면, $\angle{OAB}+22˚+32˚=90˚$이므로 $\angle{OAB}=36˚$이고,
삼각형ABO는 이등변삼각형이므로 $y=180˚-2\times{36˚}=180˚-72˚=108˚$입니다.
따라서 정답은 $\angle{x}+\angle{y}=162˚$로 2번입니다.
이렇게 삼각형의 외심의 성질에 대한 개념과 함께 문제를 풀어보았습니다.
위 문제 유형을 연습하고 싶으시면, 아래 모두매쓰 이미지 링크를 클릭하시면 문제가 새롭게 생성되고 프린트 할 수 있어요.
그럼 좋은 하루되시기 바랍니다.
중등 2학년 수학 > 삼각형의 내심과 외심 > 삼각형의 외심의 성질 연습문제 프린트 학습지
'중등 수학' 카테고리의 다른 글
| 중등 2학년 수학 > 삼각형의 내심과 외심 > 내심과 외심이 포함된 삼각형의 각의 크기 구하기 연습문제 프린트 학습지 (0) | 2024.07.15 |
|---|---|
| 중등 2학년 수학 > 이등변삼각형 > 시험 기출문제 필수 유형 연습문제 풀이 프린트 학습지 (0) | 2024.07.15 |
| 중등 2학년 수학 > 삼각형의 내심과 외심 > 직각삼각형의 빗변의 중심이 외심인 이유 연습문제 프린트 학습지 (0) | 2024.07.14 |
| 중등 1학년 수학 > 일차방정식 > 일차방정식 계산 유형 총정리 연습문제 프린트 학습지 (0) | 2024.07.14 |
| 중2 수학 > 소인수분해 > 수학 용어 및 개념정리 (0) | 2024.07.14 |