중등 2학년 수학 > 일차함수 > 연립일차방정식과 일차함수의 관계, 삼각형의 넓이 연습문제 프린트 학습지
연립방정식의 해란 무엇이고, 그것이 일차함수와 무슨 관계가 있는지 그림으로 설명하면 다음과 같습니다.
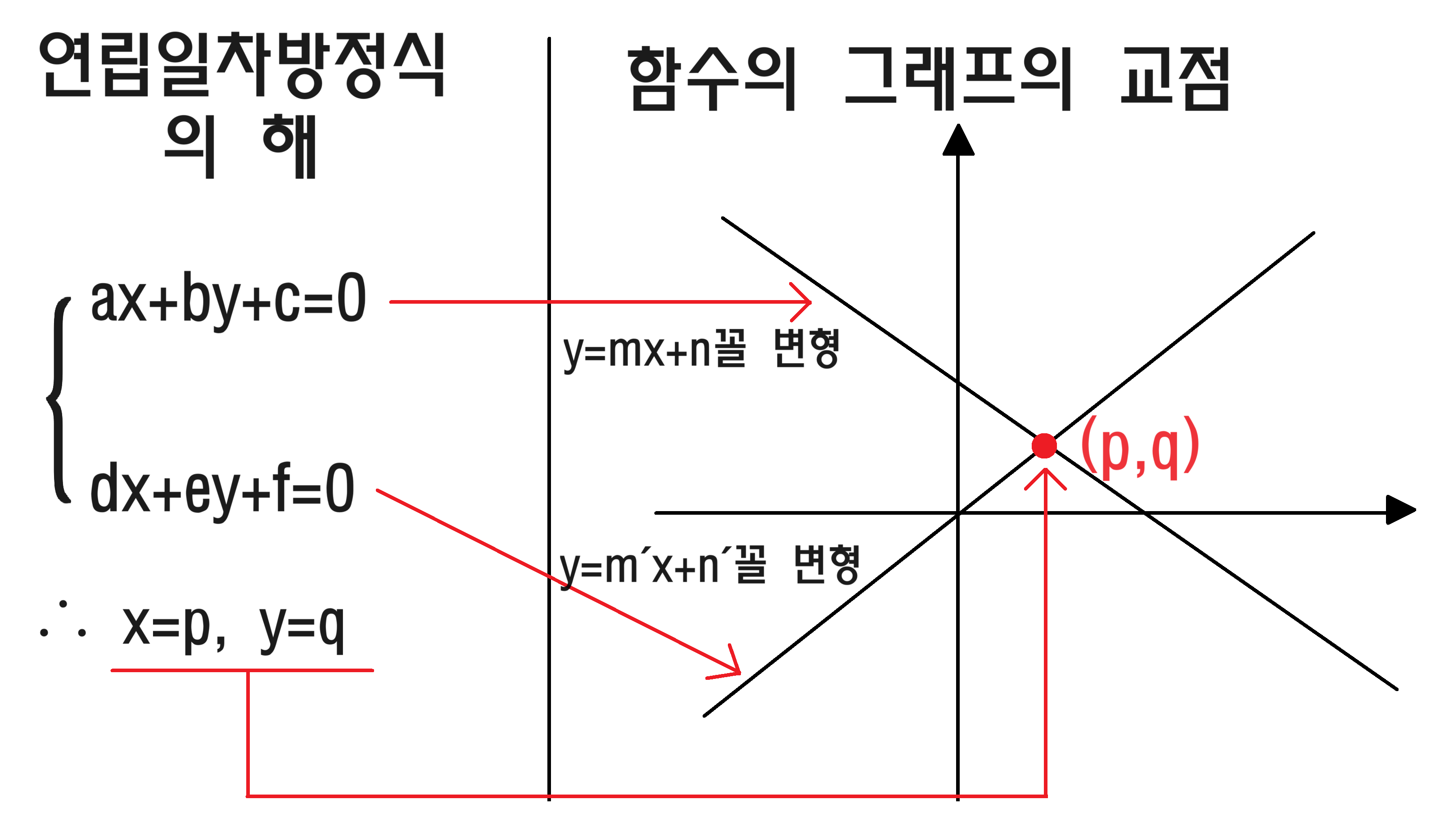
일차방정식의 해를 구하면 그것이 그래프로 나타냈을 때 교점과 같다는 사실이며, 반대로 그래프에서 교점이라 함은 각 함수식을 연립일차방정식으로 나타냈을 때의 그 해와 같다는 것입니다.
연립일차방정식의 해가 없을 수도 있나요?
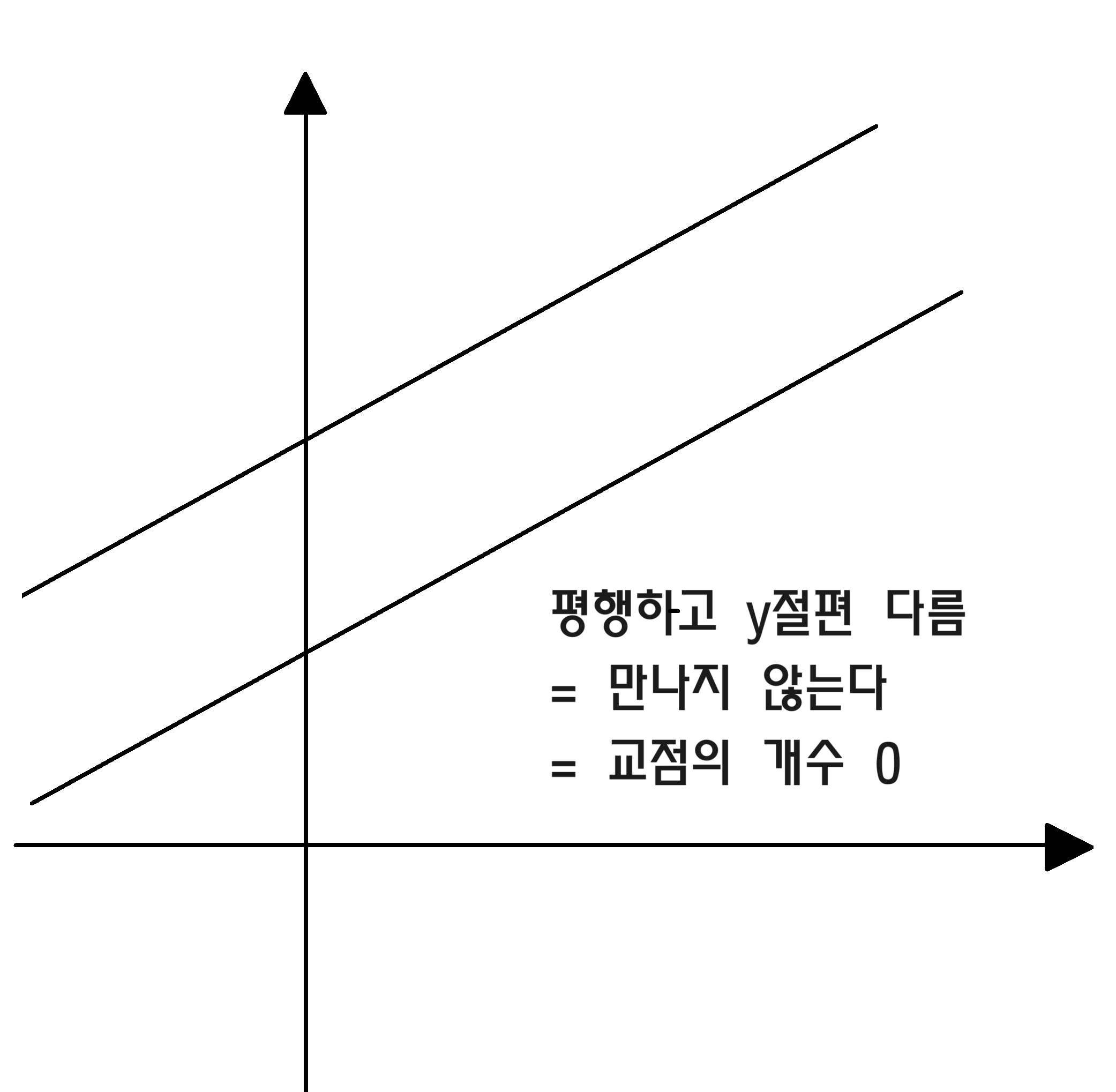
만약 다음과 같이 함수의 그래프가 서로 만나지 않는다면, 교점이 없으므로 해가 없습니다. 교점=일차방정식의 해로 생각하면 정확합니다.
그럼 실전문제를 풀어보면서 개념을 적용해보겠습니다.
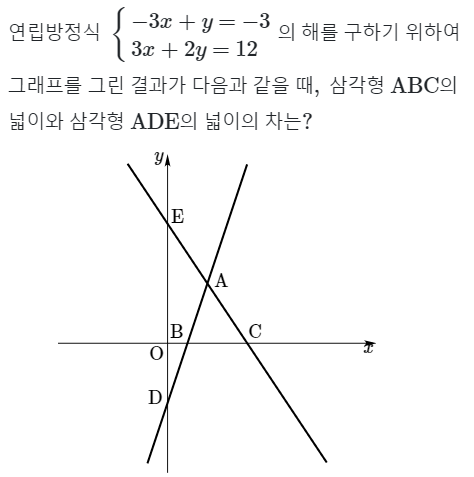
이 문제는 연립방정식의 해를 구하여 그것을 교점인 점 A의 정보로 활용하고, 나머지 B, C, D, E의 점은 x절편, y절편의 값으로 구하면 됩니다.
우선 연립방정식의 해를 구하면, 두 식을 변변 더하면 미지수 x가 사라지고 y의 값을 구할 수 있습니다.
$-3x+y=-3$
$3x+2y=12$
변변 더하면
$3y=9$
$y=3$
$y=3$을 식에 대입하면
$-3x+3=-3$
$-3x=-6$
$x=2$
이렇게 하여 연립방정식의 해가 $x=2,\ y=3$이라는 것을 알았습니다.
이제 연립방정식의 해가 두 직선의 교점의 좌표 $(2,3)$이라는 사실과 두 함수로 x, y절편을 찾으면, 아래와 같은데요,
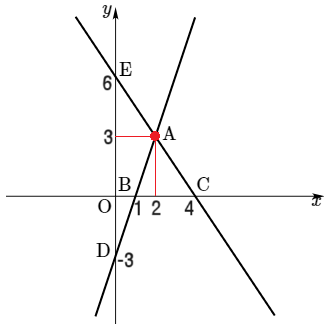
이제 삼각형ABC의 넓이와 삼각형ADE의 넓이의 차를 계산하면 됩니다.
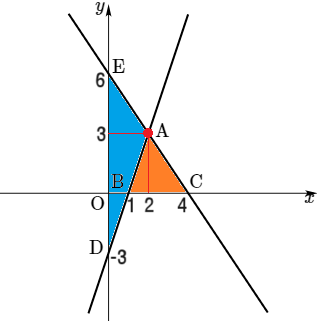
삼각형ADE의 넓이는
$\dfrac{1}{2}\times{9}\times{2}=9$
삼각형ABC의 넓이는
$\dfrac{1}{2}\times{4}\times{3}=6$
따라서 두 삼각형의 넓이의 차는 $3$입니다.
이렇게 연립방정식의 해와 일차함수의 관계 개념을 학습하고, 실전 연습문제도 풀어봤습니다.
이 개념은 너무나도 중요하기 때문에 충분히 연습하는 것이 필요한데요,
'모두매쓰'라는 사이트에서 문제를 무한히 생성해주고, 프린트할 수 있어서 개념을 학습하는데 도움이 됩니다.
그럼 오늘도 좋은 하루되세요.
[모두매쓰 생성 연습문제 예시]
중등 2학년 수학 > 일차함수 > 연립일차방정식과 일차함수의 관계, 삼각형의 넓이 연습문제 프린트 학습지
'중등 수학' 카테고리의 다른 글
| 중등 1학년 수학 > 일차방정식의 활용 > 원가, 정가, 할인, 이익 개념 연습문제 프린트 학습지 (0) | 2024.07.23 |
|---|---|
| 중등 3학년 수학 > 이차함수 > 그래프를 보고 이차항의 계수 구하기 연습문제 프린트 학습지 (0) | 2024.07.23 |
| 중등 1학년 수학 > 일차방정식의 활용 > 거리, 속력, 시간 유형 중 총 걸린 시간에 관한 연습문제 프린트 학습지 (0) | 2024.07.21 |
| 중등 2학년 수학 > 삼각형의 내심과 외심 > 삼각형의 내심의 성질 연습문제 프린트 학습지 (0) | 2024.07.18 |
| 중등 1학년 수학 > 일차방정식의 활용 > 원가, 정가, 이익 개념과 기초 연습문제 프린트 학습지 (0) | 2024.07.16 |





