중등 2학년 수학 > 삼각형의 내심과 외심 > 삼각형의 내심의 성질 연습문제 프린트 학습지
내심
삼각형의 각 꼭짓점의 각의 이등분선의 교점
내심의 성질
내심에서 각 변에 이르는 거리는 같다
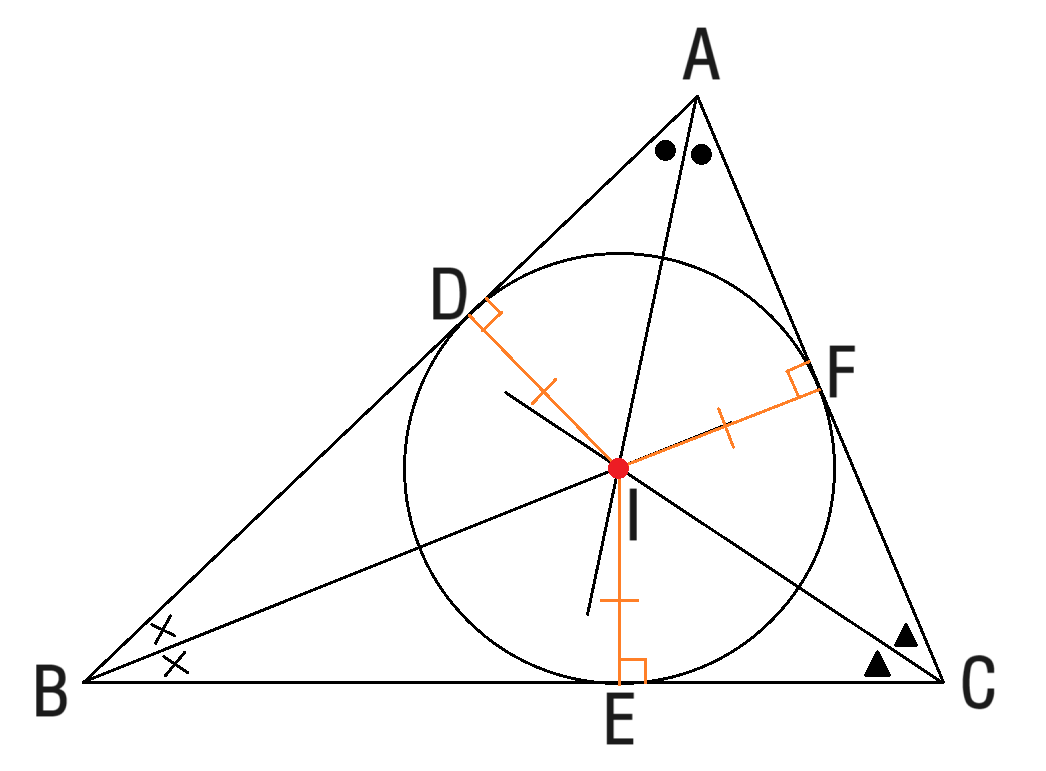
내심I에서 각 변에 내린 수선의 발을 D, E, F라 할 때, 세 쌍의 삼각끼리 RHA 합동입니다.
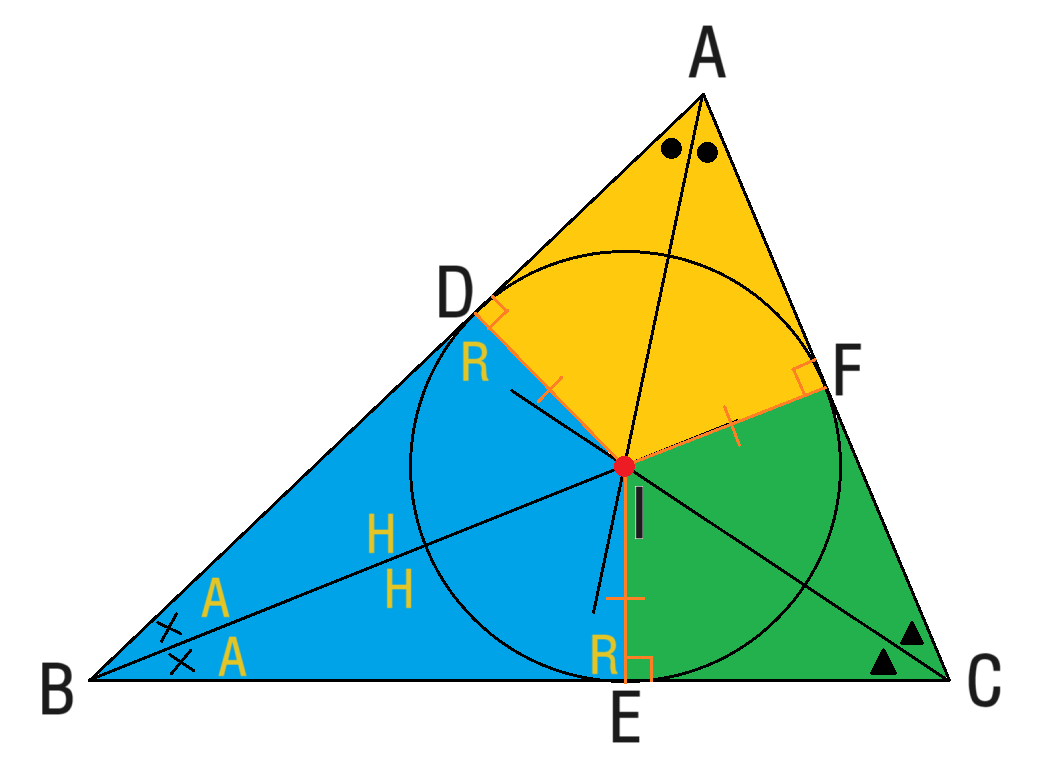
이러한 내용을 바탕으로 아래와 같은 그림을 설명할 수 있어요.
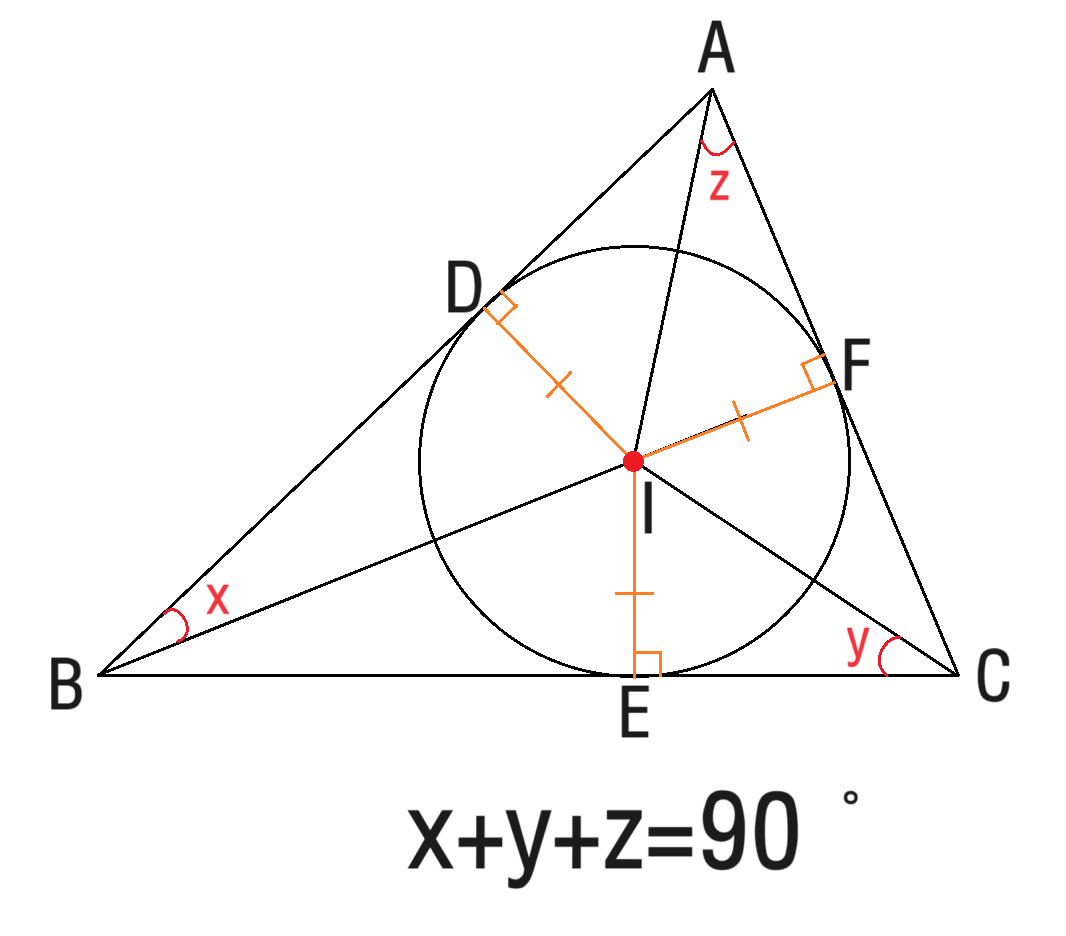
위 식이 성립하는 이유는 아래와 같아요. 각 꼭짓점에서 그은 각의 이등분으로 인해 각 꼭짓점마다 x, y, z를 하나씩 더 가지고 있고, 모두 더하면 삼각형의 세 내각의 합인 180˚와 같기 때문입니다.
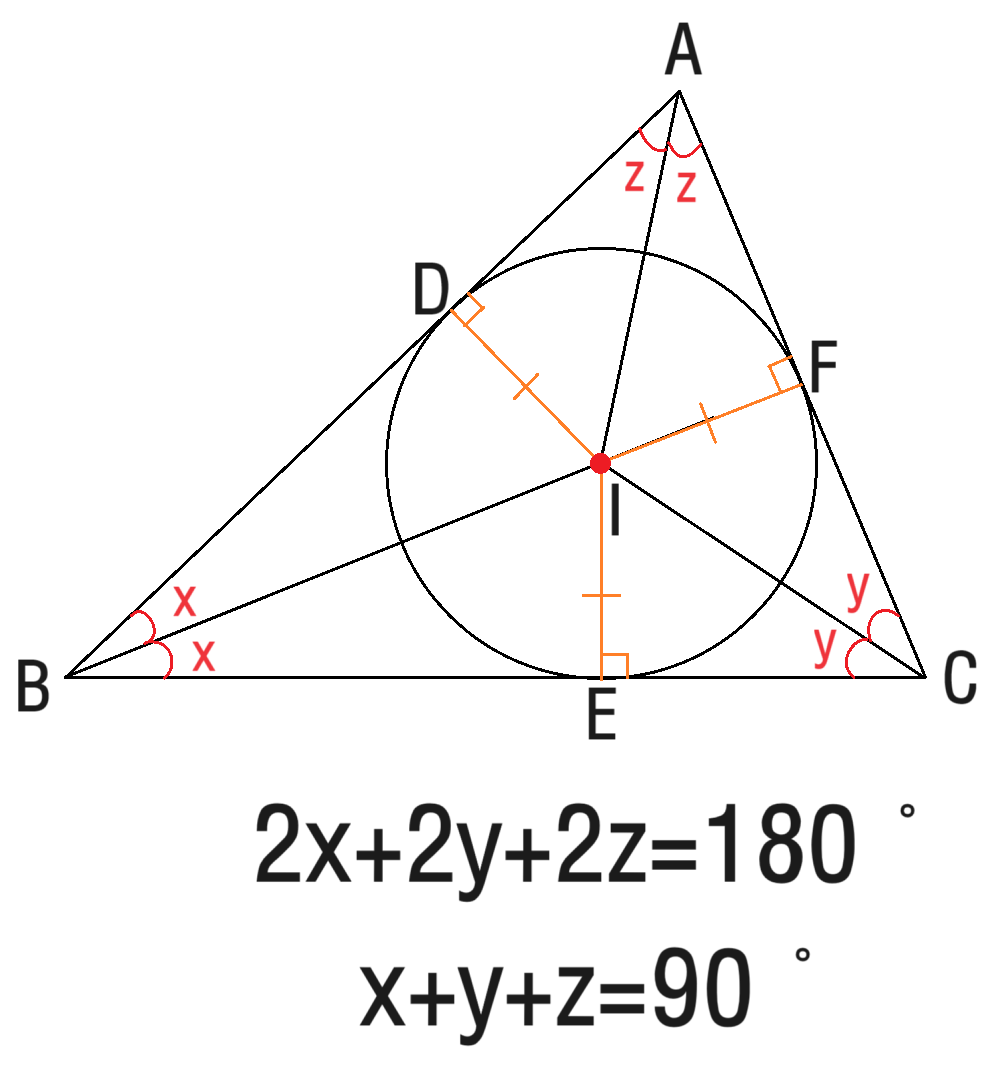
이제 개념을 활용한 문제를 풀어보도록 할게요.
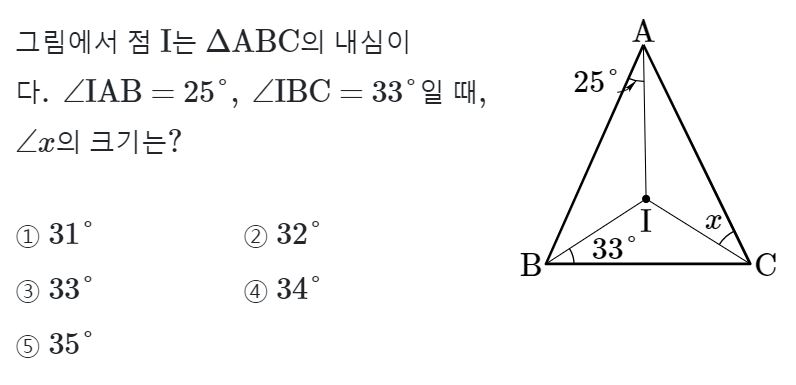
빨간색으로 색칠된 부분의 각의 합은 90˚이므로
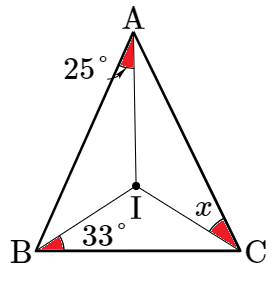
$25˚+33˚+x=90˚$
$x=32˚$입니다.
따라서 정답은 2번입니다.
문제를 하나 더 풀어보겠습니다.
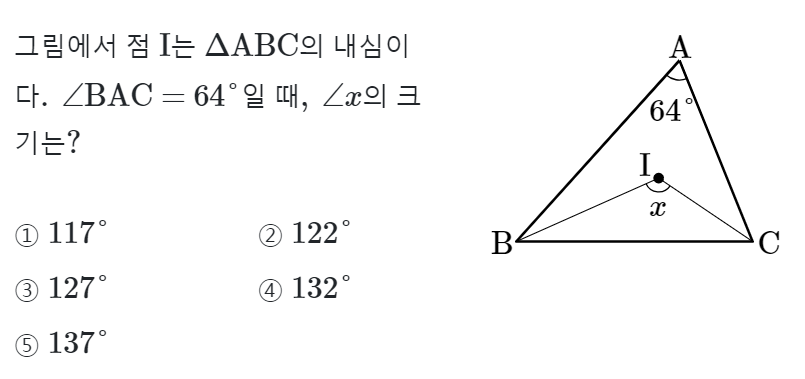
꼭짓점 B와 꼭짓점 C의 각의 이등분선의 각을 표시하면

삼각형ABC의 세 내각의 합은 180˚이므로
$2a+2b+64˚=180˚$
$2a+2b=180˚-64˚$
$2(a+b)=116˚$
$a+b=58˚$
삼각형BIC의 세 내각의 합도 180˚이므로
$a+b+x=180˚$
이때 $a+b=58˚$이므로 대입하면
$58˚+x=180˚$
$x=122˚$
따라서 정답은 2번입니다.
이렇게 삼각형의 내심의 성질에 대한 개념과 함께 문제를 풀어보았습니다.
위 문제 유형을 연습하고 싶으시면, 아래 모두매쓰 이미지 링크를 클릭하시면 문제가 새롭게 생성되고 프린트 할 수 있어요.
그럼 좋은 하루되시기 바랍니다.
중등 2학년 수학 > 삼각형의 내심과 외심 > 삼각형의 내심의 성질 연습문제 프린트 학습지
.
'중등 수학' 카테고리의 다른 글
| 중등 2학년 수학 > 일차함수 > 연립일차방정식과 일차함수의 관계, 삼각형의 넓이 연습문제 프린트 학습지 (0) | 2024.07.23 |
|---|---|
| 중등 1학년 수학 > 일차방정식의 활용 > 거리, 속력, 시간 유형 중 총 걸린 시간에 관한 연습문제 프린트 학습지 (0) | 2024.07.21 |
| 중등 1학년 수학 > 일차방정식의 활용 > 원가, 정가, 이익 개념과 기초 연습문제 프린트 학습지 (0) | 2024.07.16 |
| 중등 1학년 수학 > 일차방정식의 활용 > 거리, 속력, 시간 공식과 기초 연습문제 프린트 학습지 (0) | 2024.07.16 |
| 중등 1학년 수학 > 일차방정식의 활용 > 소금물 농도, 소금물의 양 기초 연습문제 프린트 학습지 (0) | 2024.07.16 |





