모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스
모두매쓰는 수학 문제 학습지를 무제한으로 생성하고 화면에서 즉시 풀 수 있도록 제공하는 인공지능 서비스입니다. 초등, 중등, 고등 교과서에서 다루는 핵심적인 문제들을 다양하게 제공하며
www.modoo-math.com
고등 수학(상) > 점과 좌표 > 점과 점 사이의 거리 공식, 증명, 연습문제 프린트 학습지
점과 점 사이의 거리
두 점 $A(x_1,y_1),\ B(x_2,y_2)$ 사이의 거리는 다음과 같습니다.
$$\overline{AB}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$$
점과 점 사이의 거리 공식 증명 → 피타고라스의 정리로 증명
좌표평면 위에 두 점 $A(x_1,y_1),\ B(x_2,y_2)$이 다음과 같을 때,

$x$축과 $y$축에 평행 선분을 변의 길이로 갖는 직각삼각형을 그리면,
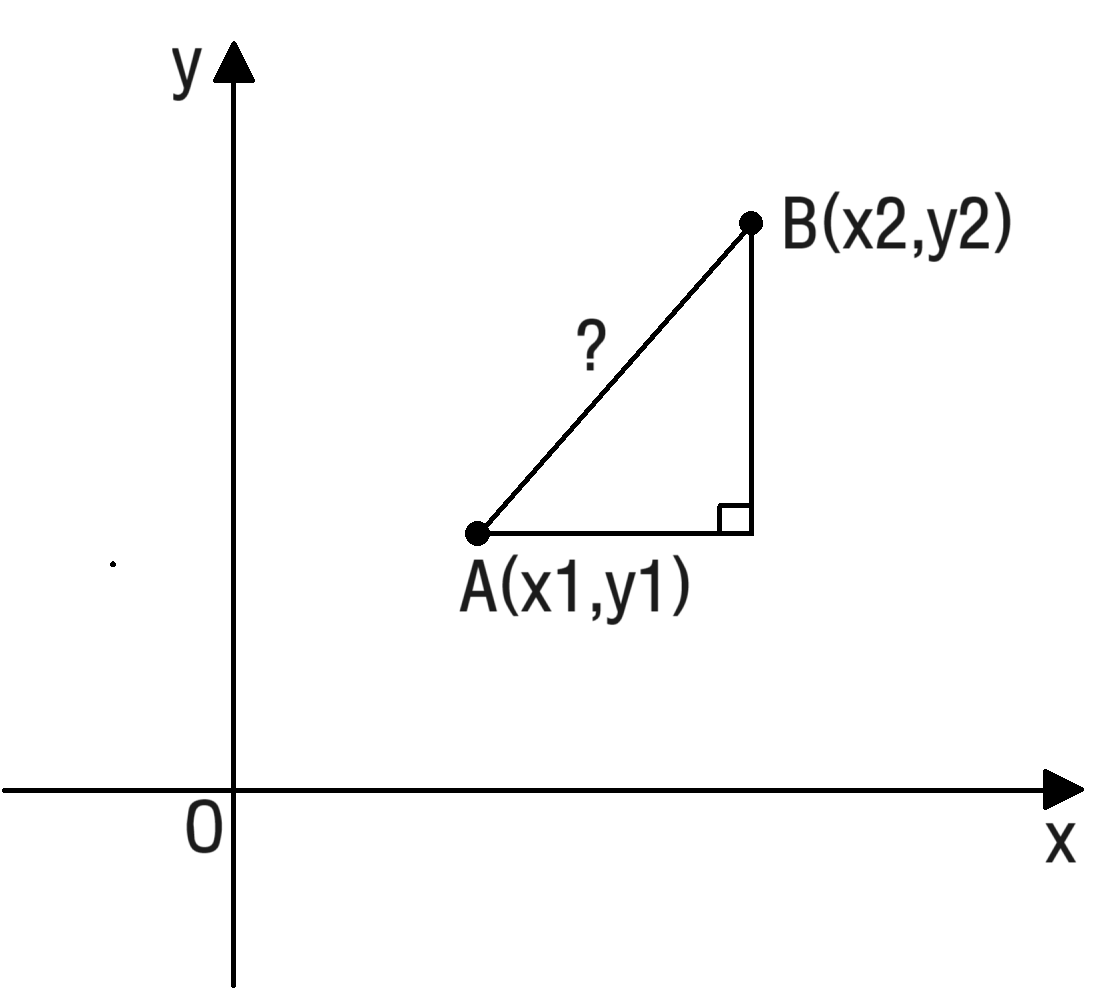
피타고라스의 정리에 의해 두 점 사이의 거리를 표현할 수 있는데요,
그러기 위해서는 아랫변과 높이를 나타낼 수 있어야 합니다.

아랫변 $\overline{AC}=|x_1-x_2|$, 높이 $\overline{BC}=|y_1-y_2|$이므로
피타고라스의 정리에 의하면
$$\overline{AB}^2=\overline{AC}^2+\overline{BC}^2$$
$$\overline{AB}^2=(x_1-x_2)^2+(y_1-y_2)^2$$
$$\overline{AB}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$$
이렇게 점과 점 사이의 거리를 증명하였습니다.
개념을 적용하는 문제를 몇 개 풀어보도록 하겠습니다.
문제1)
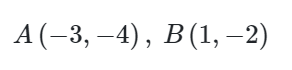
점과 점 사이의 거리 공식에 대입하면,
$\overline{AB}=\sqrt{(-3-1)^2+(-4+2)^2}=\sqrt{20}=2\sqrt{5}$
문제2)
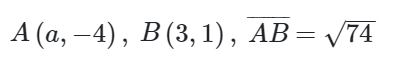
$\overline{AB}=\sqrt{(a-3)^2+(-4-1)^2}=\sqrt{74}$
양변을 제곱하면,
$(a-3)^2+25=74$
$(a-3)^2=49$
$a-3=±7$
$a=10$ 또는 $a=-4$
이렇게 하여 점과 점 사이의 거리 공식과 증명을 학습하고 문제풀이를 하였습니다.
점과 점사이의 거리 공식을 연습할 수 있는 연습문제를 풀기 위해 '모두매쓰'를 사용하시기를 추천드립니다.
모두매쓰는 초중고 수학 문제를 생성하여 프린트하는 사이트입니다.
그럼 오늘도 좋은 하루되세요.
모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스
모두매쓰는 수학 문제 학습지를 무제한으로 생성하고 화면에서 즉시 풀 수 있도록 제공하는 인공지능 서비스입니다. 초등, 중등, 고등 교과서에서 다루는 핵심적인 문제들을 다양하게 제공하며
www.modoo-math.com
고등 수학(상) > 점과 좌표 > 점과 점 사이의 거리 공식, 증명, 연습문제 프린트 학습지
'고등 수학' 카테고리의 다른 글
| 고등 수학II > 함수의 극한 > 기초 극한값 계산 연습문제 프린트 학습지 (0) | 2024.07.21 |
|---|---|
| 고등 수학(상) > 점과 좌표 > 선분AB를 m:n으로 내분하는 점과 외분하는 점 공식 연습문제 프린트 학습지 (0) | 2024.07.20 |
| 고등 수학(상) > 여러가지 방정식과 부등식 > 삼차방정식의 근과 계수와의 관계 연습문제 프린트 학습지 (0) | 2024.07.19 |
| 고등 수학(상) > 여러가지 방정식과 부등식 > 삼차방정식의 작성 연습문제 프린트 학습지 (0) | 2024.07.19 |
| 고등 수학(상) > 여러가지 방정식과 부등식 > 삼차방정식의 한 근을 알 때 나머지 두 근 구하기 연습문제 프린트 학습지 (0) | 2024.07.19 |



