고등 수학II > 도함수의 활용 > 함수의 그래프, 삼차함수 개형 3가지 개념 정리 연습문제 프린트 학습지
수학II를 잘하려면 함수의 그래프를 잘 그려야 해요. 그런데 함수의 그래프를 잘 그리기 위해서는 삼차함수 또는 사차함수의 그래프 개형에 대해 정리해둘 필요가 있어요. 그래프의 개형의 종류를 알면 함수에 대한 이해가 깊어지고 추론 능력이 생기기 때문이에요. 삼차함수의 그래프 개형은 3가지 유형이 있는데요, 삼차함수의 그래프 개형을 결정하는 것은 도함수 f'(x)의 값이 0이 되는 x값들이랍니다. 단순히 개형이 3가지라는 것을 암기하는 것으로 그치지 않고 왜 삼차함수의 그래프 개형이 3개가 나오는지까지 공부를 하면 다른 함수를 공부할 때 좋을거에요. 그럼 시작해볼게요.
도함수 f'(x)가 0이 되는 x를 찾아서..
여러분, 도함수 f'(x)의 값이 무엇을 의미하는지 잘 생각해보세요.
도함수가 무엇인가요?
도함수 f'(x) => 임의의 x에 대하여 그래프 위의 점에서의 접선의 기울기값의 함수
f'(x)는 임의의 x에 대한 접선의 기울기값이예요. 그러면 f'(x)=0은 무슨 식인가요? 바로 접선의 기울기가 0이되는 x를 구하는 방정식입니다. 다음 그림을 보면서 f'(x)가 무엇인지 직관적으로 이해해볼게요.
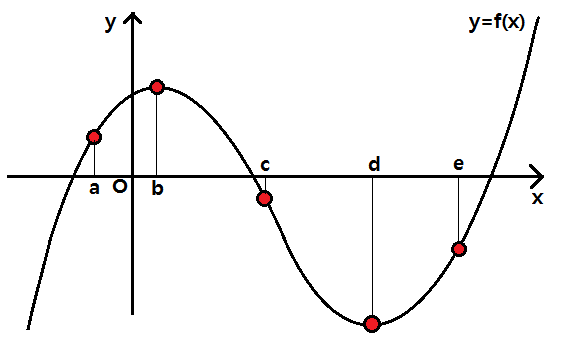
도함수 f'(x)의 x에 a, b, c, d, e를 대입할 때 각각의 값은 바로 위의 함수의 그래프 위의 점에서 접선을 그었을 때 그 접선의 기울기값과 같아요.
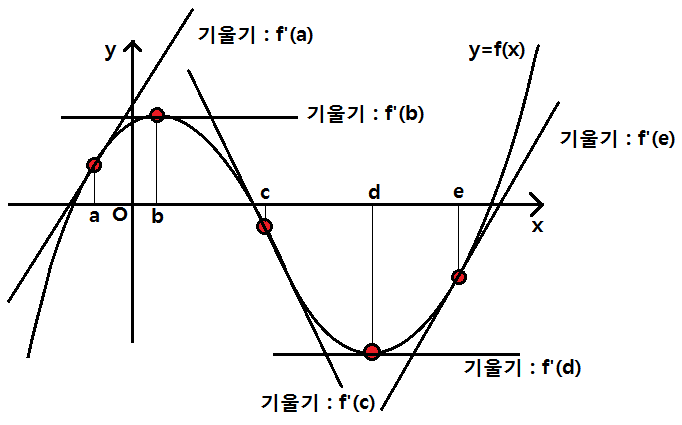
그런데 혹시 기울기가 0이라는 것이 무슨 뜻인지 모르시는 분이 있을까요?
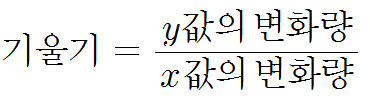
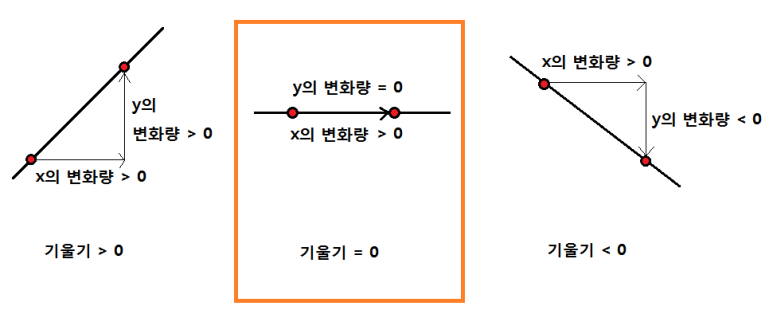
이렇게 x축과 평행한 선이 기울기가 0이라는 걸 알았어요. 그럼 다시 기울기가 0이 되는 x값을 찾아보면 x=b, x=d에서 접선의 기울기가 0이 됨을 알 수 있어요. 즉 f'(b)=0, f'(d)=0 인 것입니다.

그런데 여기서 질문. 왜 접선의 기울기가 0이 되는 b, d와 같은 x값을 다른 x값보다 특별한 이유가 무엇인가요?
f'(x)=0을 만족하는 x의 값은 극대 또는 극소의 값이 될 수 있기 때문에 특별하게 찾는거랍니다. (함수의 증감에 따라서는 극대 극소가 안될 수도 있음)
아래처럼 만약 f'(x)=0의 해를 이용해서 극대점 또는 극소점을 찾았다고 한다면,

이 점을 극대 극소로 하는 그래프를 쉽게 그릴 수 있기 때문이에요.
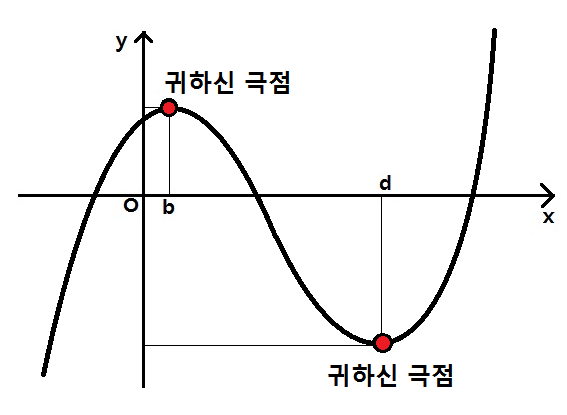
그래서 어떤 함수 f(x)이든 f'(x)=0를 만족하는 x의 해의 종류가 곧 함수f(x)의 그래프 개형 종류를 결정하게 되는거에요. 위의 삼차함수의 경우에는 도함수 f'(x)가 2개의 서로 다른 실근을 가지기 때문에 극대와 극소를 가지는 건데요, 만약 도함수 이차식 f'(x)=0의 해가 중근을 가진다면 극점을 가지지 않을 수도 있어요.
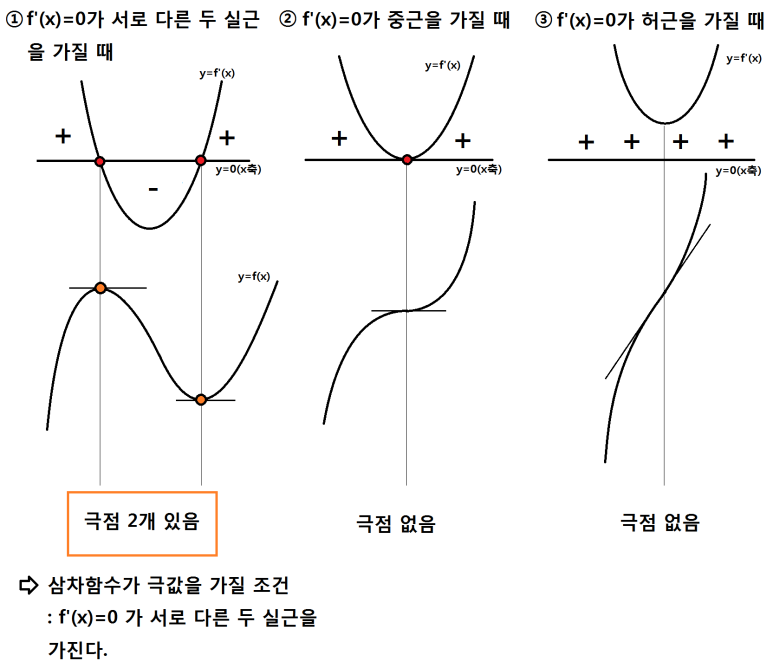
따라서 삼차함수 f(x)의 도함수 f'(x)가 x축과 만나는 점의 종류와 개수를 분류하면 3가지 유형으로 나뉘어요. 이를 x축과 이차함수와의 관계로 나타내보면,
모든 함수의 개형은 f'(x)=0 의 실근의 개수가 결정
함수의 그래프는 결국 이 함수가 어느 구간에서 증가하고 어느 구간에서 감소하는지, 그리고 어느 구간에서 가파르게 증가하고 어느 구간에서 완만하게 감소하는지 등을 그린거에요. 증가와 감소에 대한 정보는 도함수 f'(x)가 가지고 있죠.
특히 함수의 그래프에서 가장 핵심적인 정보는 접선의 기울기가 0이 되는 지점. 극대와 극소인 지점이에요.
이에 대한 정보를 가진 방정식이 f'(x)=0 이죠. f'(x)=0가 모든 함수의 그래프를 결판내는 식인거에요.
삼차함수 f(x)의 도함수 f'(x)는 이차함수이고, 이차함수가 x축과 만나는 점을 나타내는 식. f'(x)=0의 세 가지 종류가 삼차함수 개형을 말해줍니다. 다음 그림처럼요.
이제 함수의 그래프를 그리기 위해서 무조건 해야할 건 바로
- 도함수 f'(x)를 구한다.
- f'(x)=0 의 실근을 구하고, 극대 극소점을 찾는다
입니다.
삼차함수의 그래프의 개형은 f'(x)=0의 실근의 종류 세 가지와 맞물려있다는 것을 확인했어요.
다음에는 사차함수의 그래프 개형이 어떻게 결정되는지 f'(x)의 식과 함께 살펴보도록 할게요.
아 그리고 삼차함수의 개형을 연습할 수 있는 연습문제를 풀어봐야해요.
아래 이미지에 있는 링크 버튼을 누르시면, 해당 유형의 문제를 생성해줄거에요.
바로 프린트 하셔서 연습하시길 바래요.
고등 수학II > 도함수의 활용 > 함수의 그래프, 삼차함수 개형 3가지 개념 정리 연습문제 프린트 학습지
'고등 수학' 카테고리의 다른 글
| 고등 수학(상) > 여러가지 방정식과 부등식 > 삼차방정식의 작성 연습문제 프린트 학습지 (0) | 2024.07.19 |
|---|---|
| 고등 수학(상) > 여러가지 방정식과 부등식 > 삼차방정식의 한 근을 알 때 나머지 두 근 구하기 연습문제 프린트 학습지 (0) | 2024.07.19 |
| 고등 수학(상) > 여러가지 방정식과 부등식 > 삼차방정식의 계산 연습문제 프린트 학습지 (0) | 2024.07.19 |
| 수학(하) > 집합 > 원소가 n개인 집합의 부분집합의 개수의 공식과 원리 (0) | 2024.07.12 |
| 고등 수학II > 도함수의 활용 > 함수의 그래프, 사차함수의 개형 4가지 개념 정리 연습문제 프린트 학습지 (0) | 2024.07.11 |



