중등 1학 수학 > 일차방정식의 활용 > 거리, 속력, 시간 문제① - '거리'가 등식의 기준인 문제유형

중등 1학 수학 > 일차방정식의 활용 > 거리, 속력, 시간 문제① - '거리'가 등식의 기준인 문제유형

거리, 속력, 시간에 대한 문제는 공식을 몰라서 문제를 풀지 못하는 경우보다는 거리, 속력, 시간 중 어떤 것을 기준으로 식을 만들어야 하는지를 몰라서 못 푸는 경우가 많아요.

​

이번 편에서는 거리,시간,속력 중에서 거리를 기준으로 등식으로 세우는 유형​을 살펴볼게요.

​

'거리'로 등식을 세우는 유형

​

거리를 기준으로 삼아서 식을 쓰는 대표적인 유형이 바로 두 사람이 운동장이나 호숫가를 도는 유형이에요.

항상 두 사람이 등장하고, 운동장이라든지 호수와 같은 장소가 등장해요.

이때 두 사람이 '동시에' 출발을 하고 '반대방향'으로 걷기 시작할 때, 두 사람이 만날 때까지 걸린 시간을 물어보는 문제가 가장 기본문제예요.

두 사람 A, B가 둘레의 길이가 3km인 호숫가를

같은 지점에서 동시에 출발하고 반대방향으로 걷기 시작할 때,

A는 분속 50m, B는 분속 30m의 속력으로 걷는다면,

두 사람이 만날 때까지 걸린 시간은?

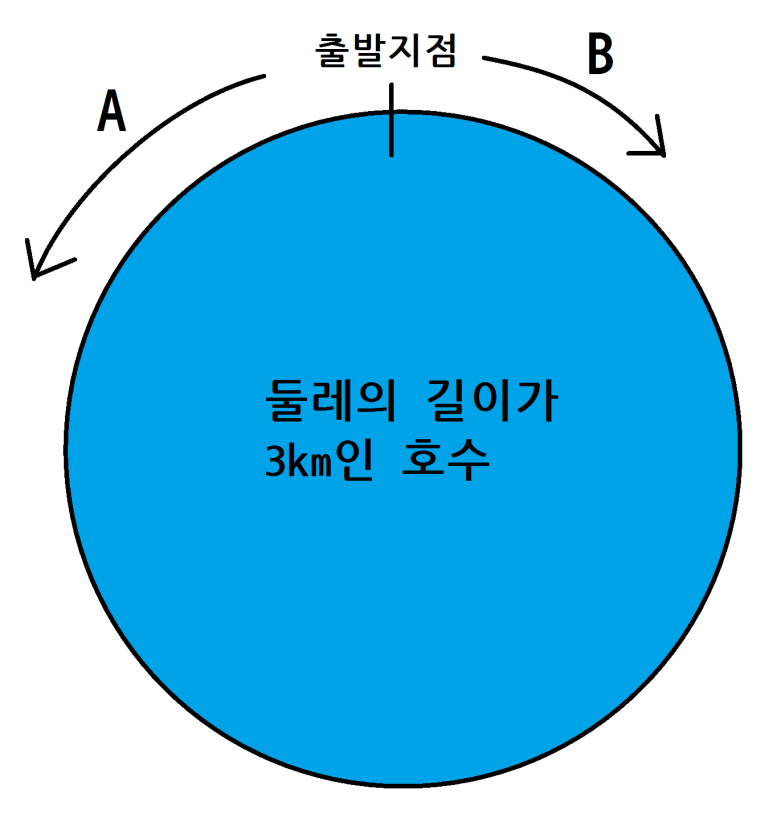
그러면 분명 두 사람은 중간 어디즘에서 만나겠죠?

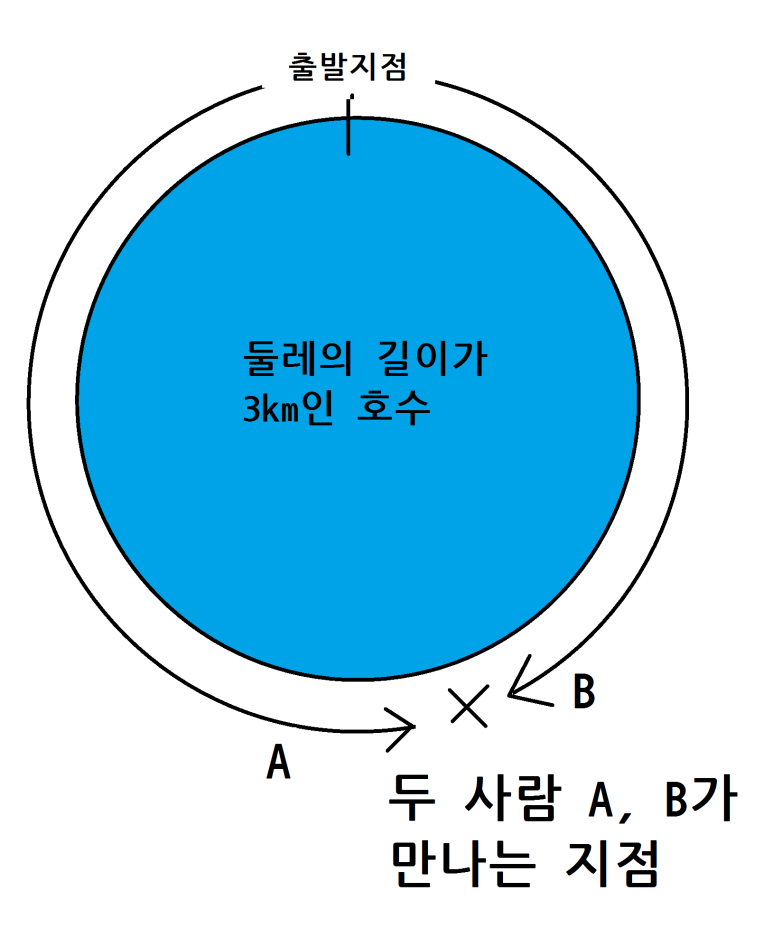
두 사람이 만나는 그때(x)까지 걸린 시간을 물어본다면 '시간으로 식을 세워야 하나?' 라고 잘못 생각할 수 있어요.

이 문제는 각자 '움직인 거리'에 초점을 맞춰야 해요. 그림을 잘 보면 A가 움직인 경로와 B가 움직인 경로 두 가지를 합치면 호수의 둘레의 길이와 같아진다는 것을 알 수 있어요.

​

A가 움직인 거리 + B가 움직인 거리 = 호수의 둘레의 길이

A가 움직인 거리를 식으로 나타내는 부분만 하면 이 식은 완성이에요.

거리 = 시간 × 속력

이므로 시간은 미지수 x, A의 속력으 분속 50m 이므로

​

A가 움직인 거리 = 50x

​

같은 방법으로 B는 동시에 출발했으니 같은 시간 x 동안 분속 30의 속력으로 움직였으므로

​

B가 움직인 거리 = 30x

​

호수의 둘레의 길이는 3km 이므로 3000m로 바꿔주면(단위를 바꾸는 이유는 분속이 m단위이기 때문에 동일한 단위로 맞춰주기 위해서예요)

​

50x + 30x = 3000

80x = 3000

x = 37.5

​

정답은 37.5분이예요.

​

'거리'가 등식을 세우는 기준이 되는 문제인지 아닌지는

문제 속에서 '만난다', '만날 때' 라는 표현이 있다는 게 팁이에요.이런 표현이 나오면 '거리'에 초점을 맞춰서 식을 세워보세요.

 

위와 같은 유형을 무제한으로 생성하여 연습할 수 있는 '모두매쓰' 사이트를 이용해보세요.

아래 링크를 달아둡니다.

​

https://www.modoo-math.com

모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스

 

중등 1학 수학 > 일차방정식의 활용 > 거리, 속력, 시간 문제① - '거리'가 등식의 기준인 문제유형